An A-Ha moment
I like puzzles. I like looking for patterns and short-cuts to solutions. I like programming. I like elegant solutions which are often the outcome of identifying a unique pattern in a specific context so I'm intrigued by the challenge of helping kids to make the leap from patterns into equations.
I've never been particularly adept at mental mathematics. I have a couple of short-cuts I use to help with estimating answers to equations but more often than not, I resort to pencil and paper or smartphone/calculator or I just do a quick estimate calculation in my head and accept that it's close enough. I never really thought much about the methods I use to do mental math until we watched Jo Boaler's video on Number talk (18 x 5) (https://www.youtube.com/watch?v=bAQQC6oZxgU) in our first 3152 class. I was stunned by how many different methods were used to arrive at the correct result and was impressed with the brilliant connection one student made to simply the question to 9 x 10. It's so obvious when you hear it but it hadn't occurred to me.
I realized that for me to solve 18 x 5, I immediately reformatted the question to be 5 x 18 because if I was going to solve it with pencil and paper I would make it look like:
18
x5
because multiplying something by a single digit is usually easier than multiplying by a double digit but that's not necessarily the case for the number 5. I was trying to find a solution as quickly as possible rather than stopping to think about the best way to solve it..
It made me think as well that how we attempt to solve the problem 18 x 5 might be different from if we're asked to solve 5 x 18. The method we choose to solve the problem may change depending on how the question is presented. The one women in the video whose solution was to round 18 up to 20, multiply by 5 and then subtract 10 illustrated this to me. This might have been more obvious if I hadn't immediately reformatted the question to 5 x 18.
While reading Jo Boaler's book, What's Math Got To Do With It, I made the connection between number sense and problem solving. I've always understood that in order to do more advanced problem solving, it's important to be very familiar with at least the 1-12 times tables. Often, recognition of patterns depends on this familiarity or at least it makes finding the solution easier or faster. What I hadn't considered was the impact that de-composing and recomposing numbers can have on problem solving.
Square numbers actually form a square! Who knew?
I never really thought about the fact that square numbers (i.e. x2) actually form a square when you draw them in a pattern or that x3 forms a cube when you form it in three dimensions with manipulatives. As far as I can recall, we didn't use manipulatives or visual representations when I learned math. It's obvious when I say it now but I don't think it had ever registered before or if it did, I never thought of the fact as having any use.
Looking at a sequence of numbers: 5, 10, 17, 26, 37, The equation that drives this sequence is not immediately obvious. If you look at the differences between the terms, you get a sequence of 5, 7, 9, 11 so it's clear that we're adding 2 more each time to an odd number but that still doesn't make the equation for the sequence obvious. However, if you draw the numbers in a pattern or use manipulatives to form them, the pattern is more obvious.


Seen this way, it becomes much more obvious that each term is composed of the square of a number plus one more. In this case, the number that is being squared is one more than the term of the sequence. So the equation would be value = (n+1)2+1. Making it visual and decomposing the number into a square component and a left-over suggests the equation.
And Rectangles are Useful Too
Where this gets even more interesting is with numbers sequences that don't contain a square. If we consider the following sequence, 7, 14, 23, 34, 47, 62 it's again obvious that the difference between the terms increases by two each time, so it's easy to predict the next term and consequently to develop a recursive algorithm that fits but it's not immediately obvious what the equation would be for predicting any nth term without knowing the previous term. However, visualization and decomposition help. Following the same approach, we draw out the numbers.

Looking at the first term, there is no obvious stand-alone square this time but instead there is a rectangle that is 2 x 3 and a stand-alone 1.
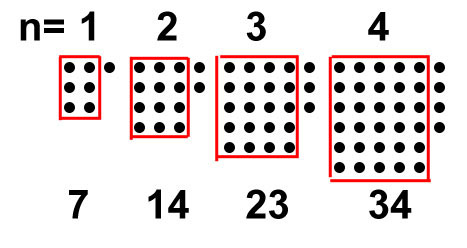
The second term is a 3 x 4 rectangle with 2 standing alone. Relating that to the value of n, we see that we're multiplying (n+1) by (n+2) and the second part of the decomposed numbers are equal to n. Therefore,
f(n) = (n+1) x (n+2) + n
f(n) = n2 +4n + 2
Representing the pattern visually, rather than trying to solve it through a strictly numerical method, suggested the solution.
Of course, this approach doesn't scale, if you get a sequence of numbers like 782, 839, 898, but having this visual understanding of what the numbers look like leads to a better understanding of the relationship between the equation f(n) = n2 +4n + 2 relates to a series of numbers.
How much further does this go?
So before this blog entry becomes a whole book that swallows up all my time with determining equations for visual patterns of numbers, I started thinking about finding more rectangles within the dots from a more complicated equation. For example, is there an approach based on this method to find the equation that represents the pattern 23, 39, 59, 83 ...? The equation is 2n2 + 10n + 11. The pattern is formed by combining dots that are (n+1)x(n+2) + (n+4)2 + n (a rectangle plus a square plus some separate dots) but I haven't determined if there's a method taking a number and figuring out what shapes are in the number. Something for another day.